Ultracold atomic gases: nonequilibrium dynamics of one-dimensional Bose gases

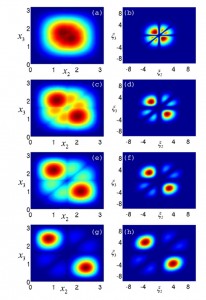
The most distinguished result is probably the formula developed for calculating the reduced one-body density matrix (which furnishes all one-body observables) for the strongly interacting 1D Bose gas (referred to as the Tonks-Girardeau gas) in Ref: R. Pezer and H. Buljan, Phys. Rev. Lett. 98, 240403 (2007). This result is important because the formula is very simple and numerically exact calculations can be made for a fairly large numbers of interacting quantum particles (say 100 and even more), and it allows insight into the strongly correlated regime, both in- and out-of-equilibrium (it is valid for time-dependent problems as well).

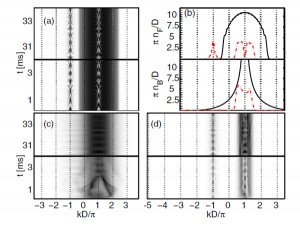
Next result is an exact study of free expansion of the so-called Lieb-Liniger gas (an interacting 1D Bose gas); D.  Jukic, R. Pezer, T. Gasenzer, and H. Buljan, Phys. Rev. A 78, 053602 (2008). Free expansion is related to time-of flight experiments. It is important to understand when interactions are present. Ref. [8] provides exact results from the weakly to the strongly interacting regime for a generic initial wave packet. Our papers on the time-dependent Lieb-Liniger gas are to the best of our knowledge first results on this topic. We have utilized and perhaps one could say brought to light an idea by M. Gaudin from the 1980s.

An interesting early paper on the range of validity of Gross-Pitaevskii theory for investigating dynamics of solitons in Bose-Einstein Condensates:

H. Buljan, M. Segev, and A. Vardi, Phys. Rev. Lett. 95, 180401 (2005).